
(Note that there are twice as many interstitial sites as anion-cation pairs but that all interstitial sites have an identical environment.) In our present notation the distance between defects i and j is.
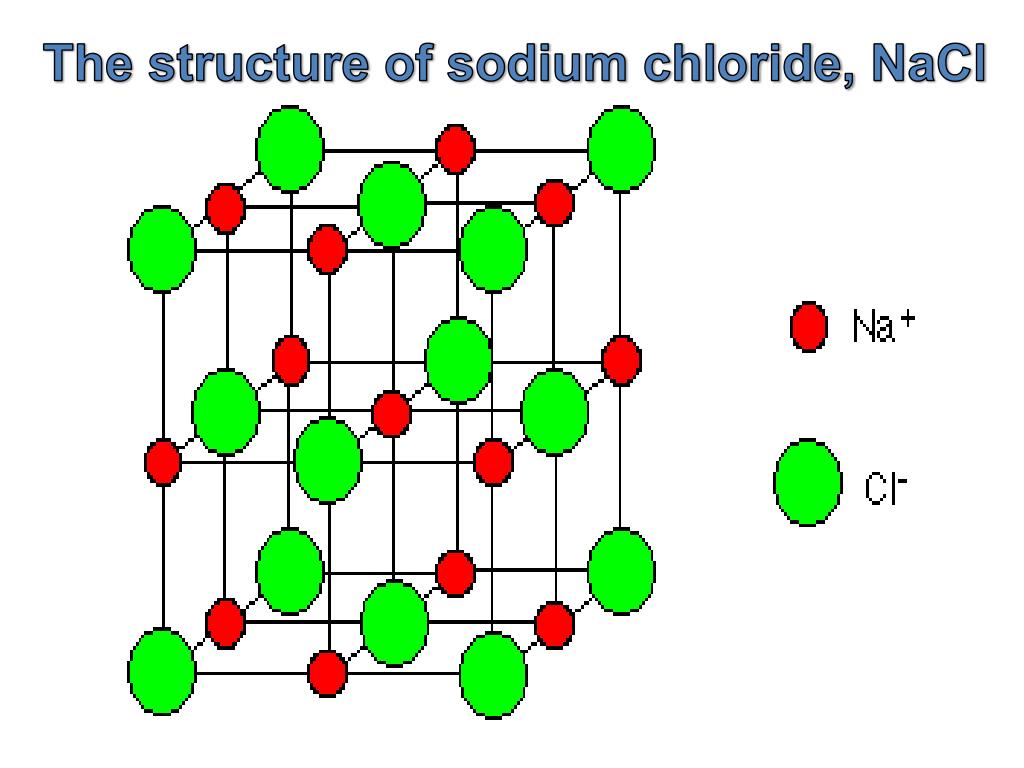
for a discussion of Frenkel disorder, then we must add two interstitial sites to the basis at (a/4, a/4, a]4) and (3a/4, a/4, a/4). However, if we wish to specify the interstitial sites of the lattice, e.g. The vectors from the origin of the unit cell to the defects i and j, which occupy positions number x and y within the cell, will be denoted X 0 and X for example, the sodium chloride lattice is built from a unit cell containing one cation site (0, 0, 0) and one anion site (a/2, 0, 0), and the translation group is that of the face-centred-cubic lattice. Thus, defects i and j are in unit cells l and m respectively, the origins of the unit cells being specified by vectors R and Rm relative to the origin of the space lattice. We now introduce a Fourier transform procedure analogous to that employed in the solution theory, s 62 For the purposes of the present section a more detailed specification of defect positions than that so far employed must be introduced. KBr crystallizes in a sodium chloride lattice arrangement with a cell edge length of 314 pm. The length of the edge of the unit cell (sometimes called the cell or lattice constant) has the value 267 pm for KF. Potassium fluoride crystallizes in a sodium chloride lattice. This value, the Madelung constant (A) for the sodium chloride lattice, could be incorporated to predict the total energy released when 1 mole of NaCl crystal is formed from the gaseous Na+ and Cl- ions. We have already mentioned that for sodium chloride approximately 1.78 times as much energy is released when the crystal lattice forms as when ion pairs form.


 0 kommentar(er)
0 kommentar(er)
